TEAMLAB

Human knowledge belongs to the world . -AntiTrust

Home PROJECT About

(12) 디버깅 보강, 배낭 문제, 동적 프로그래밍 소개

on MIT

MIT - Introduction to Computer Science and Programming in Python

Debugging 주의할 점

1. 실수를 입력값으로 받는 함수를 만들 때 , 파라메터 이름 설정 시 주의해야할 점

  • 스펠링
    1과 l을 헷갈릴 수 있음에 실수를 할 수 있다.
  • 초기화
    변수를 초기화하지 않아서 버그가 일어날 수 있다.
  • object vs value
    object와 value를 동등하게 취급해서 버그가 일어날 수 있다.
  • 별칭
    딥한 복사본 vs 얕은 복사본
  • 부작용
    함수를 호출해서 반환값을 얻고 파라메터를 최신해야하는 데 최신하지 않아서 버그가 일어날 수 있다.

2. 실수를 쫓아라

프로그램이 작동하지 않으면 실수했음을 생각해라

3.삽질을 기록해라

기록하지 않고 기억하지 못해서 삽질을 반복할 일을 없애라

4.가설들을 재고려해라

내가 생각했던 대로 프로그램이 실행이 되는지 확인하고 가설이 맞음을 확인해라

5. 주석을 수정하지말아라

다른 사람의 코드를 디버깅할 때, 코드만을 수정하고 주석에는 손대지마라

Debuggung이 어렵거나 막힐 때

1. 도움을 요청해라

버그를 고치는 것이 정말 어려울 때 도움을 요청해라.
자존심을 삼키고 주변 사람들에게 도움을 요청하고 문제가 있는 프로그램을 어떤 프로그램인지 호의를 베풀어준 사람에게 설명해야한다.

2. 쉬어라

막힌 디버깅을 멈추고 자리에서 일어나서 나 자신을 환기시키고 상쾌한 정신으로 다시 돌아와서 버그를 고치는 것을 시작해라.

버그를 찾고 고치려 할 때 무엇을 해야하는가?

  • 급할수록 돌아가라는 말이 있다.
    급하게 무언가를 하려고 하지 말아라.

  • 문제가 있는 버그를 고쳤는데 코드상 연관되어있는 다른 코드가 망가질 수 있음을 주의해라.

  • 디버깅하면서 코드를 깔끔히 정리도 해야한다.
    디버깅을 위해 다른 코드를 추가함으로써 코드를 고치는 경향이 있다. 그래서 프로그램은 점점 커진다. 이 때, 코드를 깔끔하게 정리하는 것 또한 좋은 디버깅 툴이다. 코드를 깔끔하게 정리함으로써 버그를 찾기 쉬워진다.

  • 초기 파일이나 초기 코드로 돌아갈 수 있음을 확실시 해라.
    버그를 잡으려고 오랜 시간동안 코드를 고쳤는데 막상 고치기 이전의 코드가 더 좋을 수 있다. 이 때, 내가 버그를 고치기 전의 파일이나 코드로 돌아갈 수 없다면 좌절감이 들 것이다.그래서 오래된 버전들을 저장하는 습관을 들이는 것이 좋다.

최적화

일반적으로, 모든 최적화 문제는 두가지 부분으로 나눌 수 있다. 첫 째, value를 최대화하거나 최소화하는 것이다. 둘 째, 제약조건이 있는 것이다.

기존의 최적화 문제들

  1. 최적 길 찾기 문제
    현재 위치에서 목적지까지의 최단 시간, 최단 거리 등을 고려해야한다.
  2. 여행 세일즈맨 문제
    도시 수를 주고 비행기로 도시와 도시를 여행하는 최소 비용을 찾는 문제이다.
  3. 상자 채우기 문제
    어떤 사이즈의 컨테이너를 최적화하여 채우는 문제이다.
  4. 서열 정렬 문제
  5. 배낭 문제
    배낭 문제는 한 여행가가 가지고 가는 배낭에 담을 수 있는 무게의 최댓값이 정해져있고,
    일정 가치와 무게가 있는 짐들을 배낭에 넣을 떄, 가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제이다.
    이 때, 가방에 넣을 수 있는 최대 무게가 정해져 있고 넣을 수 있는 물건의 무게와 가치가 함께 문제에서 제시된다.

continuous 배낭문제

가방에 넣을 수 있는 최대 무게 : 8 파운드
4 파운드의 금, 3 파운드의 은, 10 파운드의 건포도가 있다. 이 세 가지를 조금씩 나누어 담아 챙길 수 있다.

수식은 다음과 같다.

(MAX)  금 무게 + 은 무게 + 건포도 무게

위 수식이 제약조건인 8파운드를 넘어선 안된다.

continuous 배낭문제에서 탐욕 알고리즘이 최고의 해답을 준다.
탐욕 알고리즘은 모든 단계에서 각각의 값들을 최대화하는 알고리즘이다.

0/1 배낭문제

아이템을 조금씩 나누어 챙길 수 없고 한 개를 챙기거나 못 챙기는 binary한 문제이다.

아이템 : 시계, 라디오, 보석, 도자기, 액자 8파운드가 최대 무게이다.

  • 탐욕 알고리즘 -> 가장 귀중품을 챙긴다. 그 다음 귀중품을 챙긴다. 그 다다음 귀중품을 챙긴다. 최대 무게를 넘어가기 전까지.
    이 문제에서 최적의 알고리즘이라고 할 수 없다.

  • 무작위 알고리즘 -> 가방을 채우기 위한 모든 경우의 수를 구한다. 그러면 어떤 것이 최적의 경우인 지 알 수 있다.
    최적의 경우를 찾을 수 있지만 시간이 오래 걸린다는 단점이 있다.

무작위 알고리즘을 적용한 수식

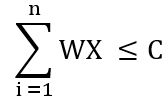
X는 0과 1로 이루어진 아이템을 표현한 벡터이다.
W는 아이템에 따른 무게이다.
WX의 예로 00000000, 00000001, 00000010 등을 예상할 수 있다.
결국, 2의 8승개의 경우가 있다.

다이나믹 프로그래밍

다루기 어려운 수를 가지는 방대한 범위의 문제들에 대해서 다이나믹 타이핑은 유용하다.
예로 들어, 최적의 하부 구조라고 일컫는 오버래핑된 sub problems들의 상황이 있다고 가정하자.

e.g.1) 피보나치 함수를 예로 들어, 오버래핑 sub problems 설명

>>> def fib(n):
...     global numCalls
...     numCalls += 1
...     print('fib called with', n)
...     if n <= 1:
...             return n
...     else:
...             return fib(n-1) + fib(n-2)
...
>>> numCalls = 0
>>> fib(5)
fib called with 5
fib called with 4
fib called with 3
fib called with 2
fib called with 1
fib called with 0
fib called with 1
fib called with 2
fib called with 1
fib called with 0
fib called with 3
fib called with 2
fib called with 1
fib called with 0
fib called with 1
5

반복적으로 같은 일을 하는 것을 오버래핑 sub problems이라고 한다. 간단한 일을 반복하는 것이지만 수를 늘리면 엄청나게 양이 늘어난다.

다음 시간엔 본 예제와는 다른 방법인 덜 다이나믹하게 늘어나는 피보나치 실행 방법에 대해 말해볼 것이다.

View Comments...