데이터를 컴퓨터에서 다루기 위해서 보통 데이터프레임 형태를 많이 사용합니다. 데이터프레임 형태는 Matrix와 비슷하게 여러 Rows와 Columns로 이루어져 있으며,
하나의 Row는 하나의 개체(Data instance)를 뜻하며, 각 Coumn은 데이터의 Feature를 의미합니다.
또한 Deep Learning의 여러 Cost Function들과 Activation Function, 머신 러닝의 여러 알고리즘 작동 원리를 이해하기 위해서는 행렬과 벡터의 이해와 그 연산에 대한
이해가 필수적이라 생각되어 짧은 지식이나마 기록하여 정리하고자 합니다.
What is Linear Equations?
선형식(Linear Equations)란, 1차항들의 다항 방정식을 의미합니다. 방정식의 최고차항은 1차항을 넘어서는 안 되며, $ xy, \, sinx,\, x^{1/2} $ 과 같은
비선형 항도 존재해서는 안 됩니다.
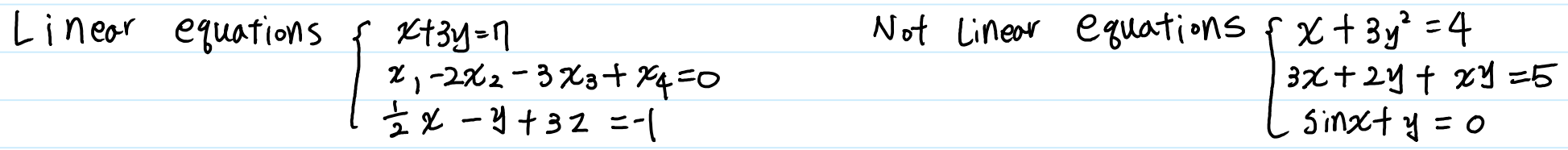
System of Linear Equations
같은 변수를 포함한 두 개 이상의 Linear Equations을 묶어 하나의 System으로 표현할 수 있습니다.
이 변수들을 미지수라고 하며, 주어진 Linear Equations을 모두 충족시키는 미지수를 해(Solution)라고 합니다.
또한 System의 해를 보다 쉽게 구하기 위해 각 방정식의 계수를 나열하여 표현하는 첨가 행렬(Augmented Matrix)에 대해 알아보겠습니다.

그런데, 이 System은 해가 없을 수도 있고, 하나의 해를 갖거나 무수히 많은 해를 가질 수도 있습니다.
이 때 하나 이상의 해를 갖는 경우를 Consistent, 해가 없는 경우를 inconsistent 라고 합니다.
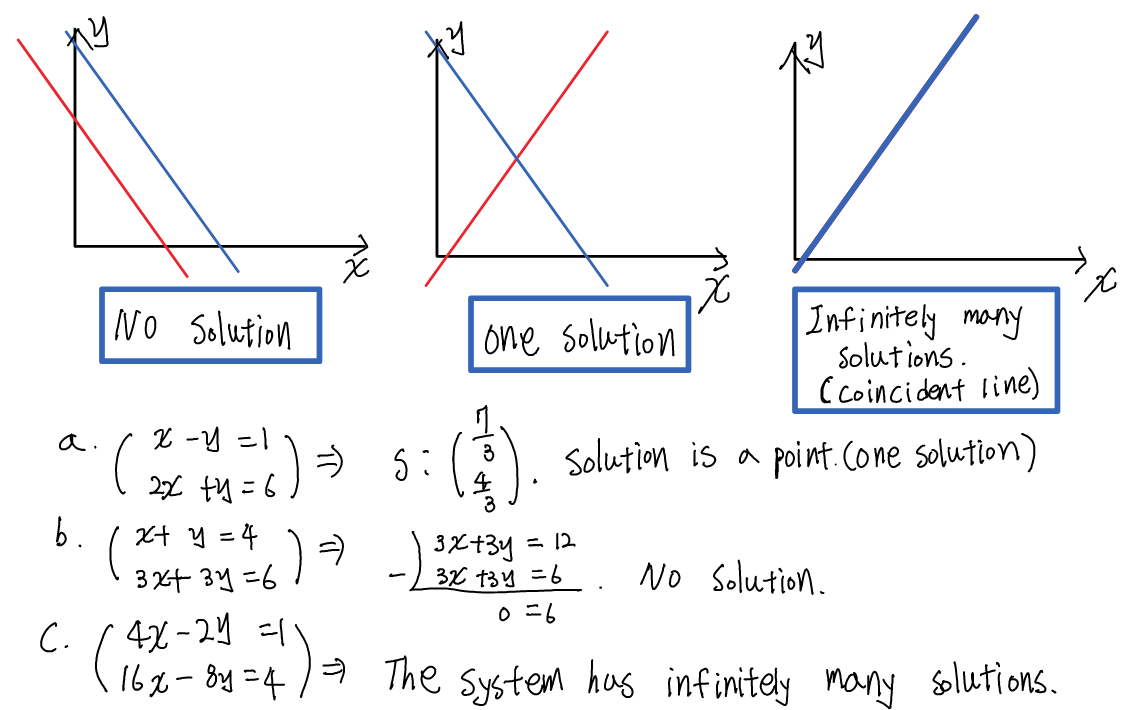
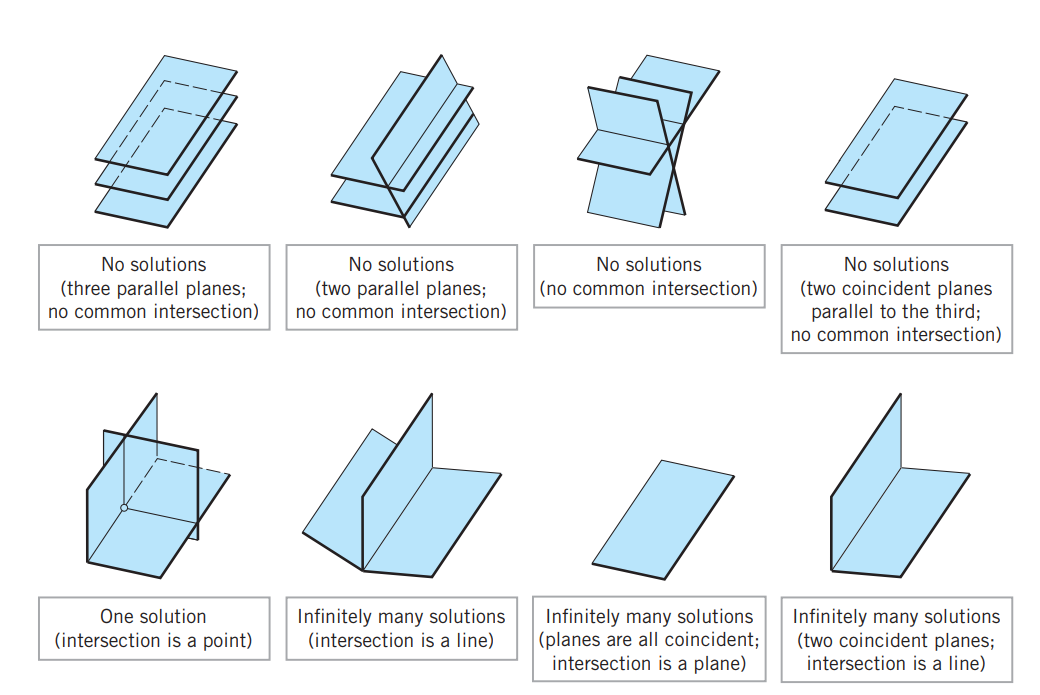
Augmented Matrix
매트릭스를 변수와 계수를 모두 곱해서 표현하는 것은 매우 번거롭고 직관적이지 못합니다. 그렇기 때문에 계수들만 표현하는 Augmented Matrix 표현방법을 주로 사용하며, 이 Augmented Matrix에 Row Operation(행 연산)을 사용하여 해를 쉽게 구할 수 있습니다.
바(|)를 기준으로 왼 쪽이 Linear System의 계수들이고, 오른 쪽은 해당 Linear combination의 상수항입니다.
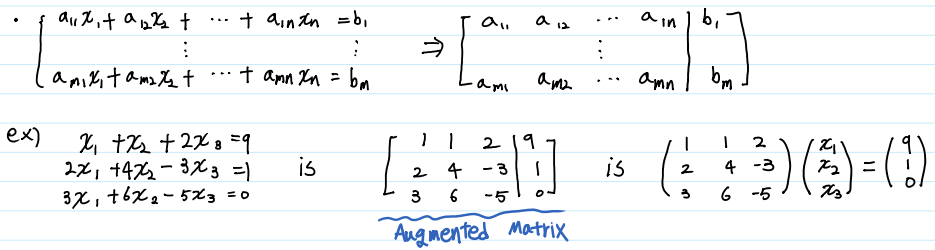
How to solve a system of linear equations.
Linear system의 해를 구하기 위한 가장 일반적인 방법은 가우스 소거법입니다. Augmented Matrix로 표현된 상태에서 세 가지 종류의 행연산(Elementary Row Operations)을 이용하여 행사다리꼴 행렬(Echelon Matrix)을 찾는 과정을 통해 해를 찾습니다.
Three Elementary Row Operations
하나의 Linear system에 대해 세 가지 기본적인 행 연산을 수행할 수 있으며, 이 세 연산을 기본 행 연산(Elementary Row Operation)이라고 합니다. 세 연산은 아래와 같습니다.
1) 한 행(Row)에 0이 아닌 상수를 곱하는 것
2) 두 행의 위치를 바꾸는 것
3) 한 행에 임의의 상수 k 를 곱해 다른 한 행에 더하는 것

Echelon Matrix
세 기본 행 연산을 통해 행사다리꼴 행렬(Echelon Matrix) 또는 기약행사다리꼴 행렬(Reduced row Echelon Matrix)을 찾음으로써
Linear System에 대한 해를 구할 수 있습니다.
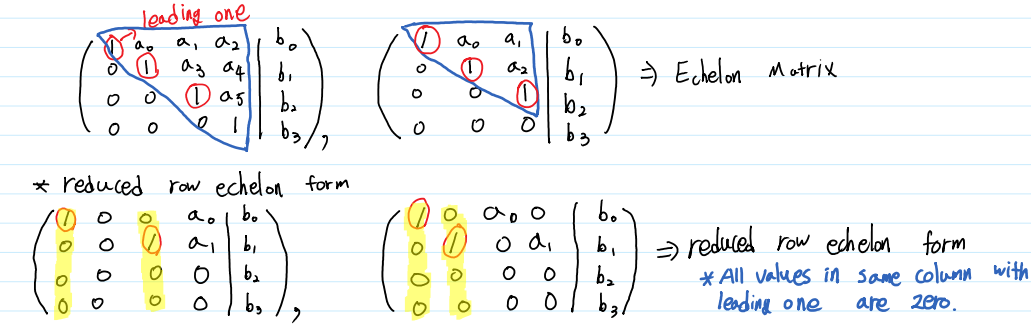
행사다리꼴 행렬이 되기 위한 조건은 다음과 같습니다.
1) 원소가 모두 0인 행은 모두 밑바닥에 위치해야 한다.
2) 원소가 모두 0이 아닌 행이 있다면, 그 행에서 0이 아닌 첫 번째 원소는 1이어야 한다. (이 때 첫 번째 원소 1을 Leading one이라고 한다.)
3) 원소가 모두 0이 아닌 행들은 위아래로 맞붙어 있어야 하며, 이 때 위 쪽의 Leading One은 아래 쪽의 Leading One보다 왼 쪽에 위치해야 한다.
위 세 조건을 만족하는 행렬을 행사다리꼴 행렬이라고 합니다. 여기에서 하나의 조건을 더 만족한다면 기약행사다리꼴 행렬이라고 표현합니다.
4) 각 행의 Leading One이 존재하는 열에서, 해당 Leading One을 제외한 나머지 원소들은 모두 0이어야 한다.
Gaussian Elimination(Gauss-Jordan Elimination)
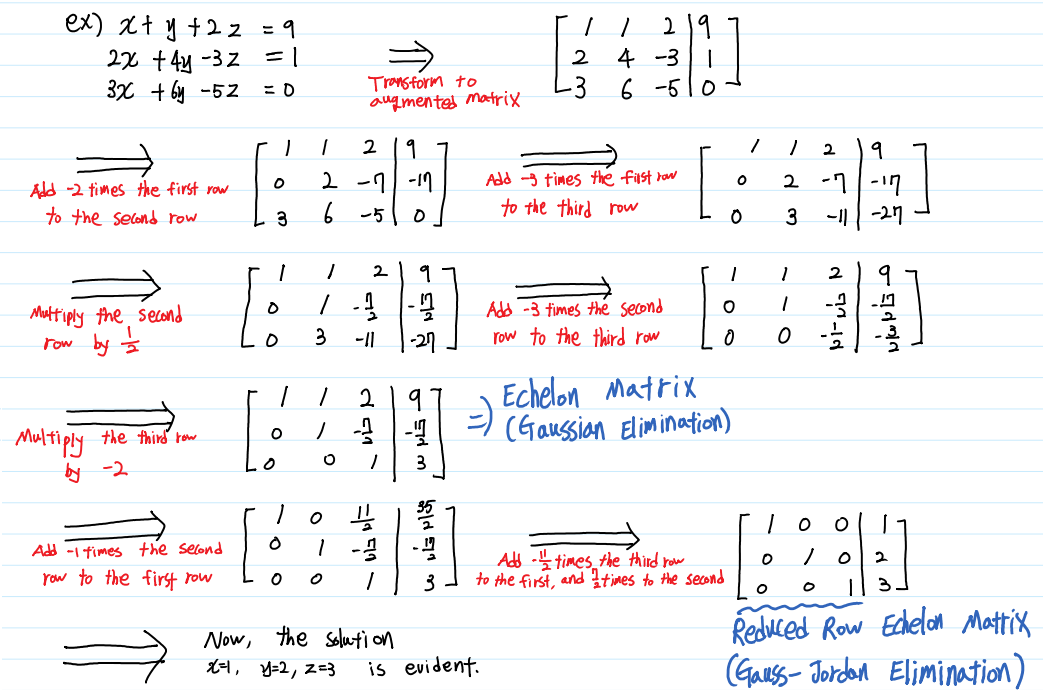
이제 Linear system의 해를 구하기 위한 준비는 모두 끝났습니다. 우리가 해야 할 일은 Augmented Matrix로 표현된 linear system을
세 가지 기본 행 연산을 통해 행사다리꼴 행렬로 표현하기만 하면 됩니다. 이 때 행사다리꼴 형태로 표현하여 해를 찾는 것을 가우스 소거법(Gaussian Elimination), 기약행사다리꼴 형태로 표현하는 것을 가우스-조던 소거법(Gauss-Jordan Elimination)이라고 합니다.
가우스 소거법은 행렬식을 찾거나 역행렬을 찾을 때에도 유용하게 사용되므로 충분히 이해해야 합니다.
Matrices and Matrix Operations
Linear system의 개념과 해를 구하는 방법에 대해 간단히 알아보았습니다. 그러나, 우리가 선형대수를 공부하는 목적은
이런 연립방정식을 쉽게 풀기 위함이 아닙니다. 데이터를 Matrix로 표현하고, 표현된 Matrix에 다양한 연산을 수행하기 위해서
Transpose, Multiplying 등 다양한 연산과 행렬식(Determinant), 특이값 분해(SVD) 등이 갖는 의미와
계산법을 알아보고자 합니다.
Square Matrix
행과 열의 수가 같은 행렬을 정방행렬(Square Matrix)이라고 합니다. 뒤에 기술할 Determinant는 Square Matrix에서만
정의되는 개념이며, 역행렬(Inverse Matrix) 역시 Square Matrix에서만 정의되는 개념입니다.
보통 행과 열의 크기 n에 따라 n차 정방행렬(square matrix of order n)이라고 표현합니다.
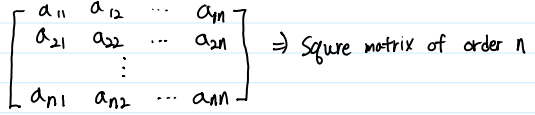
Main Diagonal
행렬의 원소 중 같은 행과 열 순서에 있는 원소들을 뜻합니다. 즉, (1, 1), (2, 2), … , (n, n)번째 원소들을 뜻하며,
반드시 Square Matrix가 아니더라도 정의되는 개념입니다. 그러나 특별히 Square Matrix 중 이 대각 원소들을 제외한
다른 모든 원소들이 0인 행렬을 대각행렬(Diagonal Matrix)이라고 부르며, 이 대각행렬 중 대각행렬이 1인 행렬을
특별히 단위행렬(Identity Matrix)이라고 합니다.

Identity Matrix는 행렬에서 곱셈의 항등원으로 사용되는 행렬이며, 일반적으로 크기 n인 단위행렬을 $ I_n $ 과 같이 표현합니다.
Addition, Subtraction and Scalar Product
크기가 같은 행렬이라면 같은 위치에 있는 원소끼리(Elementwise) 덧셈과 뺄셈 연산을 할 수 있습니다.
또한 행렬에 scalar를 곱하는 연산 역시 각 원소의 값에 scalar값을 곱하여 계산합니다. 이와 관련한 몇 가지 수학적 성질들은 다음과 같습니다.
1) $ A + B = B + A $
2) $ (A + B) + C = A + (B + C) $
3) $ (kl)A = k(lA) $ * for some constant k and l
4) $ (k + l)A = kA + lA $ * for some constant k and l
5) $ k(A + B) = kA + kB $ * for some constant k

Multiplying Matrices
앞서 크기가 같은 행렬일 때에만 연산할 수 있는 덧셈, 뺄셈과 크기에 관계없이 연산할 수 있는 scalar곱 연산방법을 알아보았습니다.
행렬과 행렬을 곱하는 것은 지금까지의 연산 방법과는 조금 다릅니다. 우선, 행렬의 곱셈은 결합법칙은 성립하지만 교환법칙은 성립하지 않습니다.
즉, $ AB \neq BA $이며, 심지어 $ AB $는 존재하더라도, $ BA $는 정의되지 않을 수 있습니다. 이에 관한 몇 가지 성질들을 알아보겠습니다.
1) $ A(BC) = (AB)C $
2) $ A(B + C) = AB + AC $
3) $ (B + C)A = BA + CA $
4) $ k(AB) = (kA)B = A(kB) $ * for some constant k
$ AB$를 연산하기 위해서는 A의 열의 수와 B의 행의 수가 같아야 합니다. 또한 연산의 결과로 A의 행의 수와 B의 열의 수의 크기를 갖는 행렬이 반환됩니다.
행렬의 곱은 A의 행과 B의 열 간의 점 곱셈(Dot product)으로 정의됩니다. 행렬간의 곱셈이 연산되는 과정을 자세히 알아보겠습니다.
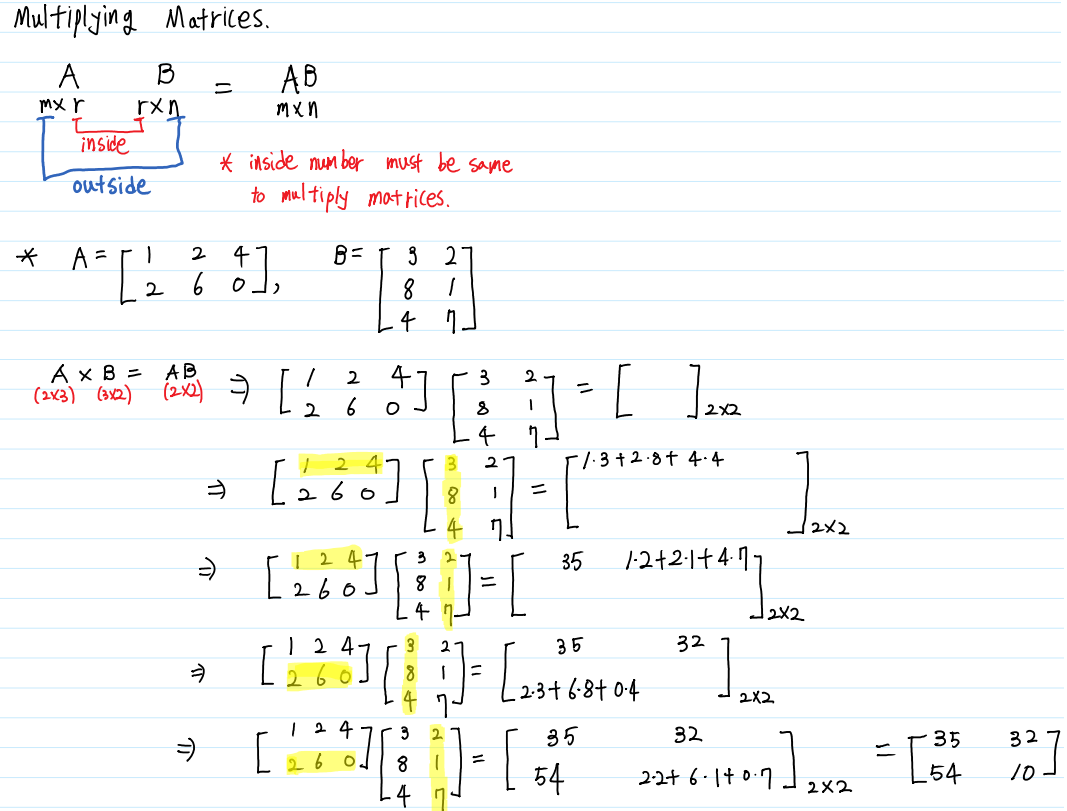
이러한 행렬간 곱의 연산법을 이용하여 Linear System을 Coefficient Matrix, Variable Vector, 그리고 Constant Vecor로 분리할 수 있습니다.
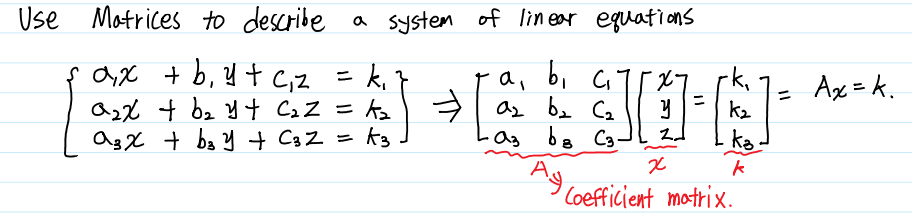
Transpose and Trace
행렬의 원소들의 위치를 이용한 두 가지 연산을 소개하겠습니다. 전치행렬(Transpose)은 앞서 공부한 Main Diagonal을 기준으로 행과 열을 바꾸는 연산입니다. 이렇게 행과 열의 바꾼 행렬을 전치행렬(Transposed Matrix)이라고 하며, 행렬 A에 대한 전치행렬은 $ A^T $로 표현합니다.
전치 연산에는 몇 가지 특징이 있습니다.
1) $ (M + N)^T = M^T + N^T $
2) $ (cM)^T = cM^T $
3) $ (M^T)^T = M $
4) $ (MN)T = N^TM^T $
5) $ (M^T)^{-1} = (M^{-1})^T $ if $ M^{-1} exists
특히 4), 5)의 경우 다양한 증명 등에 사용되므로, 익혀두는 것이 좋습니다.
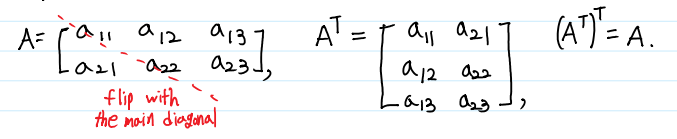
대각합(Trace)의 경우 좀 더 이해하기 쉽습니다. 우선, Trace는 Square Matrix에서만 정의 됩니다. 연산하는 방법은, 그냥 Square Matrix의 모든 대각원소들을 합해주면 됩니다.
Trace에 대해서도 몇 가지 특징이 있습니다.
1) $ tr(A^T) = tr(A) $
2) $ tr(cA) = ctr(A) $ * for some constant c
3) $ tr(A + B) = tr(B + A) $
4) $ tr(A - B) = tr(B - A) $
5) $ tr(AB) = tr(BA) $
Inverse of matrix
앞서 곱셈의 항등원인 단위행렬(Identity Matrix)에 대해 배웠습니다. 실수 공간의 역수처럼 행렬에서도 단위행렬을 만들어 내는 역원을 역행렬(Inverse Matrix)이라고 합니다.
즉, $ AB = I_{n} $을 만족하는 B를 A의 역행렬이라고 부르며, A는 Invertible Matrix(가역행렬)라고 부릅니다. 역행렬은 다음의 세 가지 동치인 조건을 가지기 때문에 A를 B의 역행렬이라고도 할 수 있습니다.
1) $ AB = I_{n} $
2) $ BA = I_{n} $
3) $ AB = BA = I_{n} $
A가 Invertible Matrix(가역행렬)일 때, A의 역행렬 B를 $ A^{-1} $과 같이 표현하며, 역행렬은 다음과 같은 성질들을 만족합니다.
1) $ (A^{-1})^{-1} = A $
2) $ (kA)^{-1} = k^{-1}A^{-1} $ * for some scalar k
3) $ (AB)^{-1} = B^{-1}A^{-1} $
이제, 2x2 매트릭스의 역행렬을 구하는 방법을 시작으로, 앞서 공부했던 Row Operations를 통해 3차원 이상의 역행렬을 구하는 방법도 알아보겠습니다.
우선, Square Matrix 가 Ivertible Matrix가 되기 위해서, 다음과 같은 조건을 만족해야 합니다.
$ad - bc \neq 0$
여기에서 를 A의 Determinant(행렬식)이라고 하며, Determinant는 행렬에서 매우 중요한 개념이므로, 다음 장에 자세하게 기술하겠습니다.
Sqaure Matrix가 조건을 만족한다면, 2차원 행렬에서는 역행렬을 쉽게 구할 수 있습니다.
원소 a와 d의 위치를 바꾸고, b와 c에 -를 붙여주기만 하면 쉽게 구할 수 있습니다.
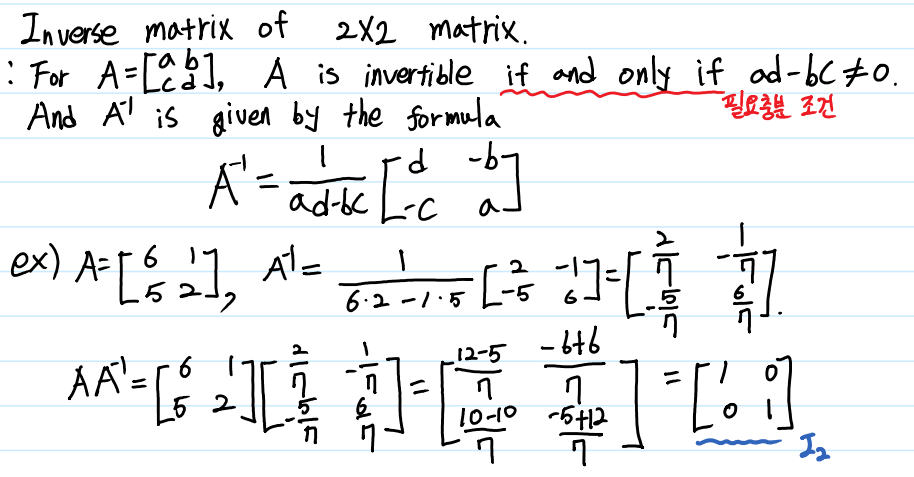
만약 2차원 Square Matrix A가 Invertible이라면, 다음과 같은 과정을 통해 Linear System의 해를 쉽게 구할 수 있습니다.
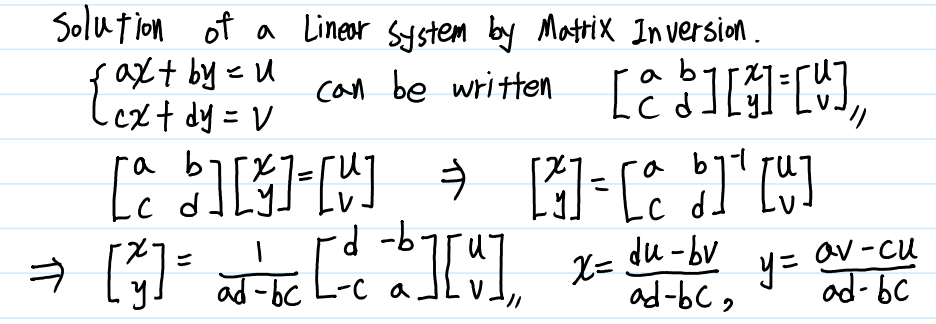
2차원 Matrix의 역행렬은 이처럼 비교적 어렵지 않게 구할 수 있습니다. 그러나 3차원 이상의 Matrix의 역행렬을 구하는 것은 2차원 행렬의 역행렬을 구하는 것 만큼 쉽고 직관적이지 않습니다.
우선, 우리가 앞서 배운 Row Operations를 이용하여 역행렬을 구하는 방법을 배워보겠습니다.
특별히 다른 점은 없습니다. 우리가 구하고자 하는 행렬 A의 오른 쪽에 같은 차원의 Identity Matrix를 붙인 후, 구분이 쉽도록 |를 긋기만 하면 역행렬을 구할 준비가 끝난 것입니다. 이제 행렬 A에 대하여 Gauss-Jordan Elimination을 실행하여 행렬 A를 Identity Matrix로 만들면 됩니다. 단, 이 과정에서 하나의 행이라도 모든 원소가 0인 행이 생긴다면, 그 행렬 A의 Determinant는 0이며, 역행렬이 존재하지 않는 non invertible 행렬이 됩니다.

Determinants
Determinant(행렬식)이란 Square Matrix에서만 정의되는 개념으로, 행렬 A에 대한 행렬식은 $ det(A) $와 같이 표현합니다.
해당 행렬이 표현하는 Linear System이 유일한 해를 갖는지를 판단하기 위해 사용되지만 이외에도 해당 행렬의 선형 변환이 나타내는 부피 등 다양한 기하학적 의미를 가지고 있으며, 이후에 배울 Eigenvalue(고유값)과 Eigenvector(고유 벡터)를 계산하는 데에도 사용되는 매우 중요한 함수입니다.
Determinant가 갖는 여러 성질들에 알아본 후 이를 쉽게 계산하는 방법에 대해 알아보겠습니다.
1) $ det_I = 1 $
2) $ det(AB) = detAdetB $
3) $ det(cA) = c^ndet(A) $ * *for some constant c, n is size of matirx
4) $ detA^{-1} = (detA)^{-1} $
5) $ detA^T = detA $
Minors and Cofactors
Determinant에 대해 배우기 전에 Minor(소행렬)과 Cofactors(여인자)에 대해 먼저 알아보겠습니다. Minor는 행렬의 특정 한 행과 한 열을 제외한 나머지 행렬의 행렬식을 의미하며, i번째 행과 j번째 열을 제외한 나머지 행렬식을 $ M_{ij} $이라고 표현합니다.
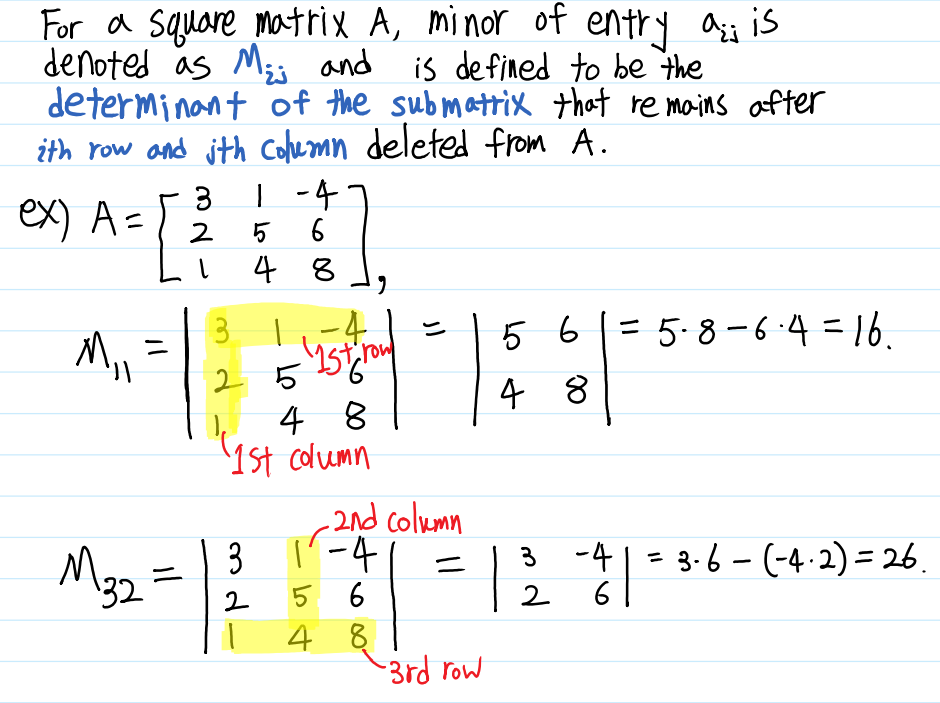
Cofactor는 Minor에 $(-1)^{i+j}$를 곱하면 된다. 즉, 행과 열을 뜻하는 i, j를 더해서 이 수가 짝수이면 더하고, 홀수이면 빼면 됩니다.
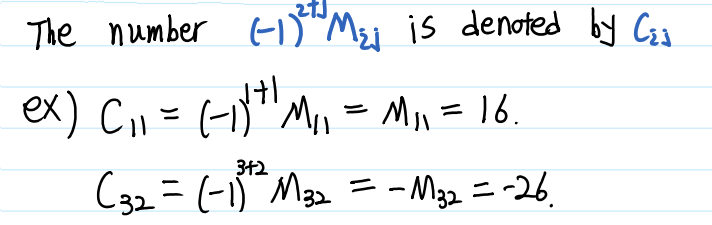
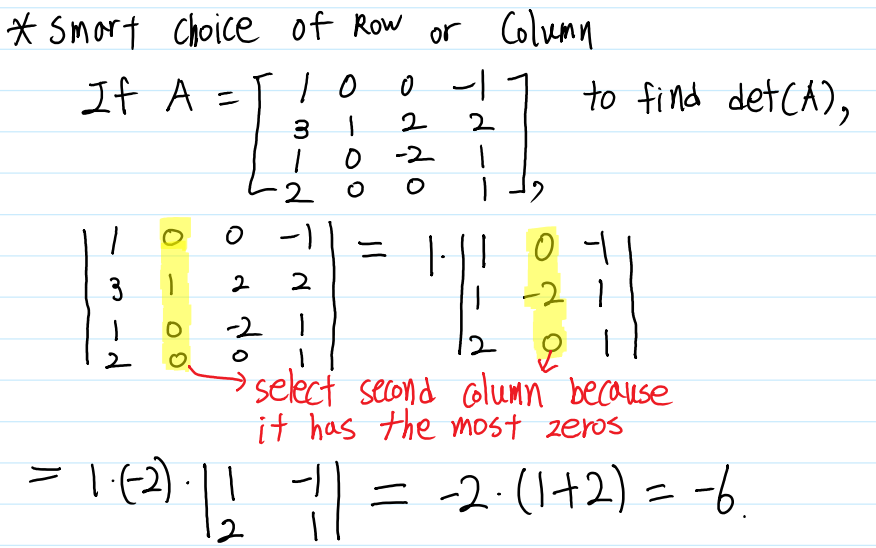
Minor와 Cofactor에 대해 이해했다면, 이제 Cofactor를 이용하여 Determinant를 구하는 방법에 대해 알아보겠습니다. Minor와 Cofactor에 대해 잘 이해했다면, 이 계산식 역시 그리 어렵지 않게 느껴질 것입니다. Cofactor를 구할 때 행렬 내 하나의 원소를 기준으로 구했다는 것을 기억하고 계실 것입니다. Determinant를 구하는 것은 하나의 원소가 아니라 하나의 행 또는 열을 선택하여 해당 행, 열에 있는 모든 원소들의 Cofactor를 더함으로써 행렬식을 구할 수 있습니다. 이 과정을 Cofactor expansion(여인자 전개) 혹은 Laplace expansion(라플라스 전개)이라고 합니다.

여전히 계산식이 복잡하게 느껴질 수도 있습니다. 하지만 하나의 행과 열을 선택하여 계산할 수 있으므로 0이 많은 행과 열을 선택하여 전개한다면 훨씬 쉽게 Determinant를 구할 수 있을 것입니다.
또, 앞서 배운 Row Operations를 이용하여 더더욱 쉽게 Determinant를 구할 수 있습니다. 이 연산을 수행하기 위해 우선 특별한 형태의 행렬을 새로 배우겠습니다. Main Diagonal을 기준으로 한 쪽에만 원소가 존재하고, 나머지 원소들은 0인 행렬을 Triangular Matrix(삼각행렬)이라고 부릅니다. Triangular Matrix의 Determinant는 항상 Main Diagonal들의 곱으로 정의됩니다.

삼각행렬의 형태를 보시면 우리가 앞서 배웠던 행사다리꼴 행렬과 비슷하다는 것을 알 수 있습니다. 앞서 우리가 Row Operations을 통해 해를 찾았던 것 처럼, Determinant도 Row Operations를 통해 쉽게 구할 수 있습니다. 행렬의 Row Operations와 거의 비슷하지만, Determinant의 Row Operations는 약간의 차이점이 있습니다.

이제 Determinant에 Row Operations를 수행하여 삼각행렬 형태로 만들어 주기만 하면 됩니다.

부록으로, 2x2, 3x3 Matrix에서 쉽게 사용할 수 있는 사뤼스 도식에 대해 설명하겠습니다. 파란 화살표는 더하는 항이고, 붉은 화살표는 빼는 항입니다. 3x3행렬에서는 첫 번째와, 두 번째 열을 행렬의 우측에 붙인 뒤 화살표를 그려서 계산합니다.
Eigenvalue and Eigenvector
Eigenvalue(고유값)와 Eigenvector(고유벡터)는 다음과 같은 식을 만족하는 상수 $ \lambda $와 벡터 $ x $를 뜻합니다. 이 때의 상수 $ \lambda $를 Eigenvalue, 벡터 $ x $를 Eigenvector라고 하며 기하학적인 의미로 (Linear Transformation)선형 변환을 실시할 때 크기만 변하고 방향은 보존되는 벡터가 존재하는데, 이 때 변하는 크기가 Eigenvalue, 보존되는 벡터가 Eigenvector입니다.(참고) 데이터 분석에서도 PCA 등 여러 알고리즘에 사용되고, 후에 기술할 SVD의 기초가 되는 개념이기 때문에 잘 이해하시는 것이 좋습니다.
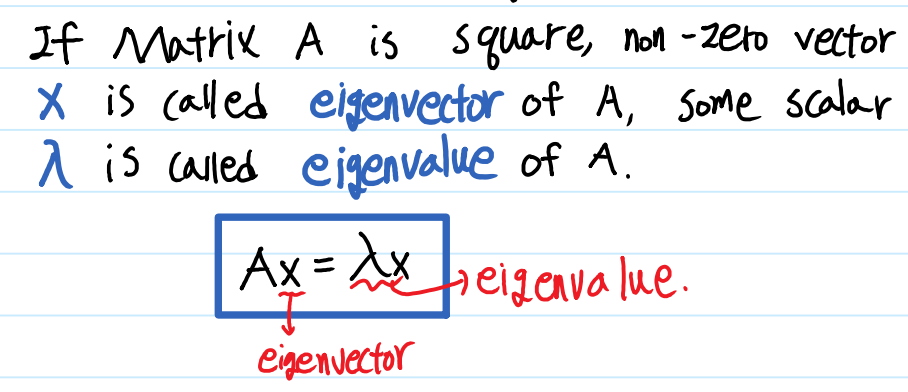
위 식에서 좌변을 우변으로 이항한 뒤, x로 묶어 표현하면 $ (\lambda I - A)x = 0 $과 같이 표현할 수 있으며, 여기에서 $ \lambda I - A $의 역행렬이 존재한다면, 이 식의 해는 항상 $ x = 0 $이므로 $ \lambda I - A $는 역행렬이 존재해서는 안 됩니다. $ det(\lambda I - A) = 0 $ 을 만족하는 $ \lambda $찾음으로써 Eigenvalue를 구할 수 있으며, 행렬식 $ det(\lambda I - A) = 0 $ 을 Characteristic equation이라고 합니다.

Characteristic equation을 통해 Eigenvalue를 찾았다면, 식 $ (\lambda I - A)x = 0 $ 을 통해 해당 Eigenvalue와 짝을 이루는 Eigenvector를 찾을 수 있습니다. 만약 행렬 A의 Eigenvalue가 $ \lambda_1, \lambda_2 $와 같이 구해졌다면, $ \lambda_1 $에 해당하는 Eigenvector를 $ x_1 $, $ \lambda_2 $에 해당하는 Eigenvector를 $ x_2 $와 같이 표현할 수 있습니다.
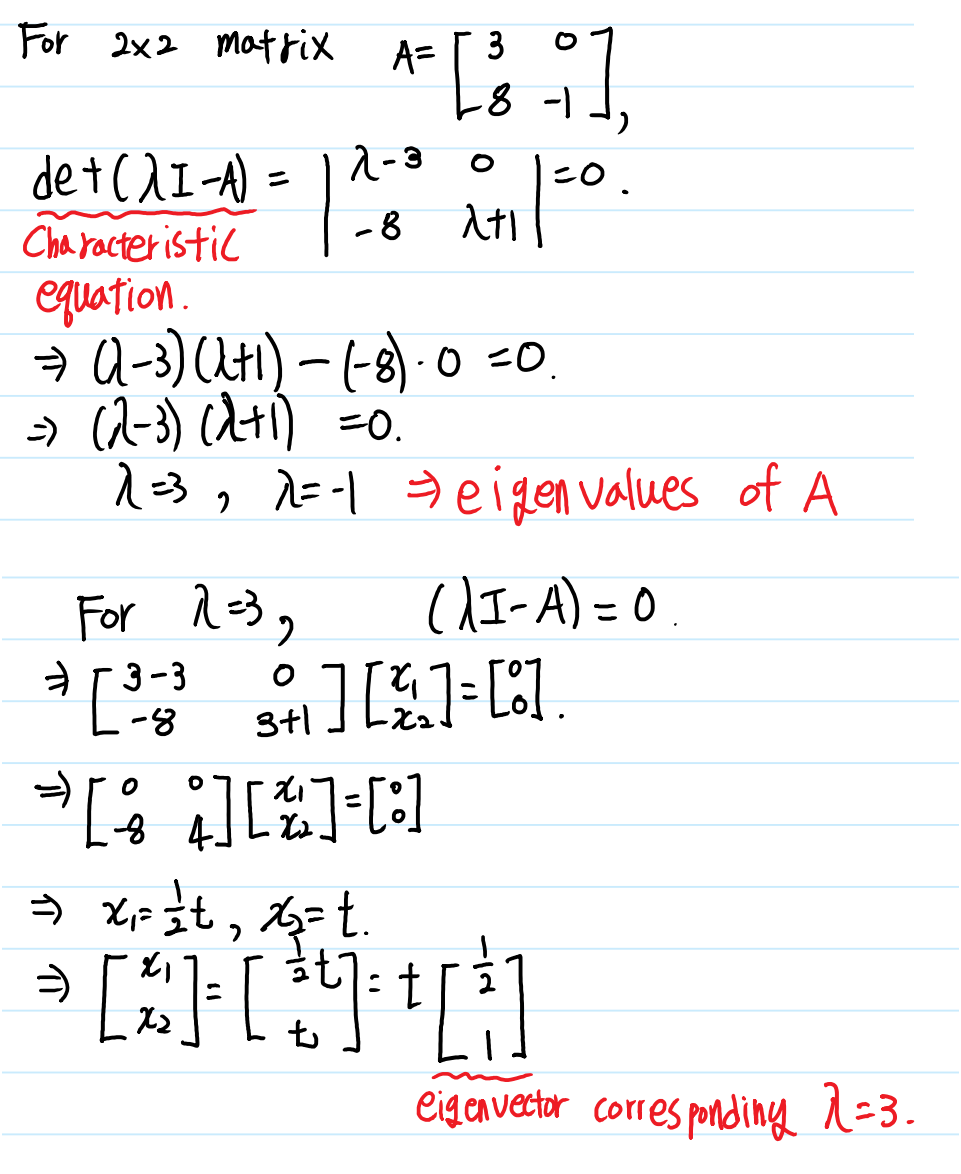
아마 Eigenvector를 구하는 과정에서 무언가 이상하다는 것을 느끼셨을 것입니다. 앞서 설명한 대로 Eigenvector는 방향이 보존되는 벡터이기 때문에 같은 방향을 나타내고 크기만 다른 수없이 많은 벡터들이 존재합니다. 따라서 하나의 벡터로만 정의하지 않고 방향을 나타낼 수 있도록 정의합니다.(일반적으로는 크기가 1인 벡터를 사용합니다.)
Linear Independent & Rank
어떤 한 Linear system에 대해, 각 벡터들의 선형 결합이 존재하지 않는 경우를 Linear Independent(선형 독립)이라고 합니다. 즉, 어떤 벡터도 다른 벡터들의 조합으로 설명되지 않는 경우를 말하는데, 어떤 경우를 얘기하는지 예시를 통해 알아보겠습니다.

예시의 Linear System에서, v1이 v2와 v3의 선형 결합으로 표현될 수 있기 때문에 선형 독립이 아닙니다.
이제 Rank(계수)의 개념에 대해 알아보겠습니다.
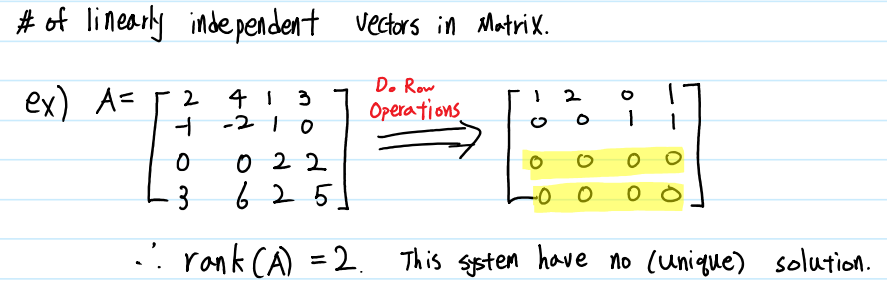
Rank란, 하나의 행렬에서 Liner Independent한 벡터의 수로 정의할 수 있습니다. 예시의 Liner System에서 독립인 벡터의 수가 2개이므로 이 벡터의 Rank는 2이며, 이는 $ rank(A) = 2 $와 같이 표현합니다. 만약 크기가 $n$x$n$인 Matrix $A_{n*n}$에서 $rank(A) = n$이라면, 그 matrix는 invertible이고, 따라서 $det(A) \neq 0$이며, 행렬 A는 유일한 해를 갖습니다.
Diagonalization
만약 어떤 행렬 A가 주어졌을 때,
1) A가 n개의 선형 독립인 Eigenvector를 갖는가?
2) $D = P^{-1}AP$를 만족하는 invertible P가 존재하는가? (D는 Diagonal Matrix)
라는 질문을 한다면, 매트릭스의 Diagonalization(대각화)가 완벽한 답변이 될 수 있습니다. Square Matrix $A_{n*n}$에 대해 n개의 Eigenvalue가 있는 경우, A는 대각행렬로 분해가 가능합니다.
대각행렬은 Determinant의 계산의 편의, 역행렬 계산의 편의 등이 있기 때문에 어떠한 행렬을 대각행렬로 분해하는 것은 계산을 쉽게 만들어 주는 매우 중요한 방법 중 하나입니다.

이 때 P는 각 column이 Eigenvector인 matrix이고, D는 각 Diagonal 원소들이 Eigenvalue인 matrix입니다. 주의해야 할 점은, P의 i번째 열에 i번째 Eigenvector가 사용되었다면, D의 i번째 행에도 i번째 Eigenvalue가 사용되어야 한다는 것입니다.
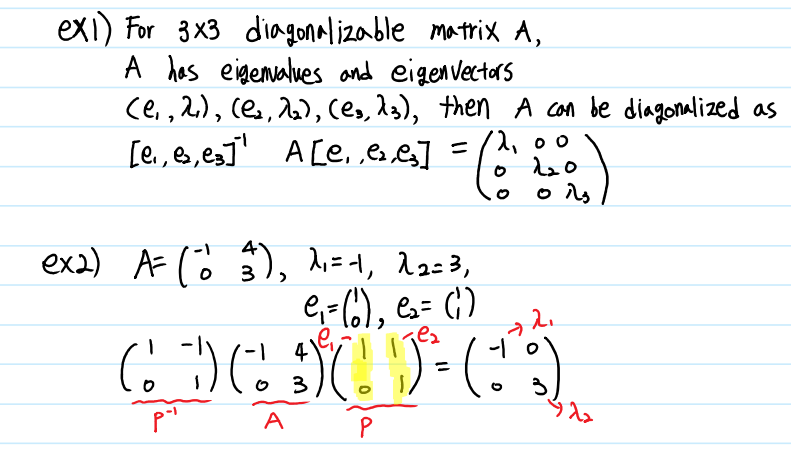
Singular Vector Decomposition
드디어 대망의 Singular Vector Decomposition(SVD, 특이값 분해)를 공부할 차례입니다. 앞서 공부한 Diagonalization은 Square Matrix에서만 사용할 수 있다는 큰 단점이 있습니다. 그러나 우리가 마주하는 거의 모든 데이터들은, Instance의 수와 Feature의 수가 다른 경우가 대부분입니다. 따라서 데이터 자체를 Diagonalization하는 것은 거의 불가능합니다. 하지만 SVD는 Square Matrix가 아니더라도 사용할 수 있는 방법입니다. Diagonalization과 비슷하게 Matrix를 Diagonal Matrix로 분해한다는 것은 같지만, 이 때 사용되는 P가 Matrix 자체의 Eigenvector를 사용하는 것이 아니라 $A^TA$의 Eigenvector와 Eigenvalue를 사용한다는 점이 다릅니다.
Orthogonal Matrix
SVD를 배우기 전에 Matrix의 Orthogonality(직교)에 대해 먼저 공부하겠습니다. Orthogonal Matrix란, Matrix A에 대해 $A^{-1} = A^T$인 Matrix를 뜻합니다. 즉, $A^TA = AA^T = I$인 Matrix로, 자기 자신의 i번째 row와 i번째 column을 곱했을 때에만 1이 되고 $i \neq j$인 i번째 row와 j번째 column에 대해서는 0이 되기 때문에 직교행렬이라고 불립니다.

SVD
이제 이 포스트의 마지막 개념인 SVD에 대해 알아볼 차례입니다. 우선, SVD는 어떤 Matrix를 Diagonalization과 유사하게 Singular Value와 Singular Vector로 분해하는 것입니다. 여기서 Singular Value란 어떤 Matrix A에 대해 $\sqrt{\lambda_i(A^TA)}$를 뜻합니다. ($\lambda_i(A^TA)$란 $A^TA$의 i번째 Eigenvalue를 의미)
그리고 Singular Vector 역시 어떤 Matrix A에 대해 $\lambda_i(A^TA)$의 Eigenvector를 Right Singular Vector, $\lambda_i(AA^T)$의 Eigenvector를 Left Singular Vector라고 합니다. (Singular Value는 $A$와 $A^T$의 순서와 관계없이 같습니다.)

Eigenvector를 Left와 Right으로 나누어 부르는 것은 SVD를 수행할 때 Eigenvector들로 이루어진 Matrix의 위치 때문인데, 예시를 통해 설명하겠습니다.

Left Singular Vecotor들이 $\sum$의 왼 쪽에 위치하고, Right Singular Vecotor들이 오른 쪽에 위치하는 것을 볼 수 있습니다. 여기에서 U와 V는 Orthogonal Matrix이므로, $A = U \sum V^T$는 $\sum = U^TAV$와 같이 표현할 수 있습니다.
이렇게 공부한 선형대수가 과연 Data Science의 어디에 쓰이는지 많이 궁금하시리라 생각됩니다. 대표적으로 주성분분석(PCA), 소셜 네트워크 분석, 추천 시스템의 Matrix Factorization, 데이터 압축 등에 사용됩니다. 이외에도 많은 알고리즘이 선형대수를 알고 있어야만 이해하기 쉽습니다.
선형대수의 기본 개념과 연산, 분해방법에 대해 알아보았습니다. 사실, 벡터의 내적(Inner Product, Dot Product)과 외적(Outer Product), 벡터 공간(Vector Space)등 면밀히 알아보지 않은 개념들도 많습니다. 그러나 이 것을 공부하는 것은 이 글을 읽는 여러분의 몫으로 남겨두고 포스트를 마치고자 합니다.
읽어주셔서 감사합니다.
References 티스토리 블로그 ‘다크 프로그래머’ 위키백과 Howard Anton, Chris Rorres, Elementary Linear Algebra with supplemental applications, 2014